Let’s Build A Simple Interpreter. Part 1.
“如果你不知道编译器是怎样工作的, 那么你就不知道计算机是怎样工作的. 如果你不是100%确定你是否知道编译器怎样工作, 那么你就不知道它们是怎样工作的.” – Steve Yegge
就是这样. 思考一下. 你是新手还是经验丰富的软件开发者并不重要: 如果你不知道编译器和解释器怎么工作, 那么你就不知道计算机怎么工作. 就是这么简单.
那么你知道编译器和解释器怎么工作吗?
我的意思是, 你是100%确定自己知道它们怎样工作的吗? 如果你不是.

或者你不是并且对此感到很激动.

不要担心. 如果你坚持看完这个系列并和我一起搭建一个解释器和编译器, 那么你最后就会知道它们是怎么工作的.
并且你也会成为一个自信快乐的人. 至少我希望如此.

为什么你要学习解释器和编译器? 我会给出三个理由.
-
为了编写一个解释器或编译器, 你必须有很多的你需要一起使用的技术技能. 编写一个解释器或一个编译器将会帮助你提高这些技能, 从而成为一个更好的软件开发者. 同样, 你将学习的这些技能在编写任何软件中都有用, 而不只是编译器或解释器.
-
你真的很想知道计算机是怎么工作的. 解释器和编译器通常看起来很像魔法. 而你不该觉得这些魔法理所当然. 你想要解密构建一个解释器和编译器的过程, 理解它们怎么工作, 然后掌握这些东西.
-
你想创造自己的编程语言或领域特定语言. 如果你创造了一个, 你就需要为它创造一个编译器或解释器. 最近, 对新的编程语言的兴趣出现了复苏. 你可以看到几乎每天都有新的编程语言出现: Elixir, Go, Rust 只是一小部分.
好吧, 但什么是解释器和编译器呢?
编译器和解释器的目标是把某种高级语言的源程序翻译成另一种格式. 非常模糊, 不是吗? 先忍一下, 在后面的系列中你会学到源程序到底被翻译成了什么.
这时, 你可能也想知道编译器和解释器有什么区别. 就这个系列而言,
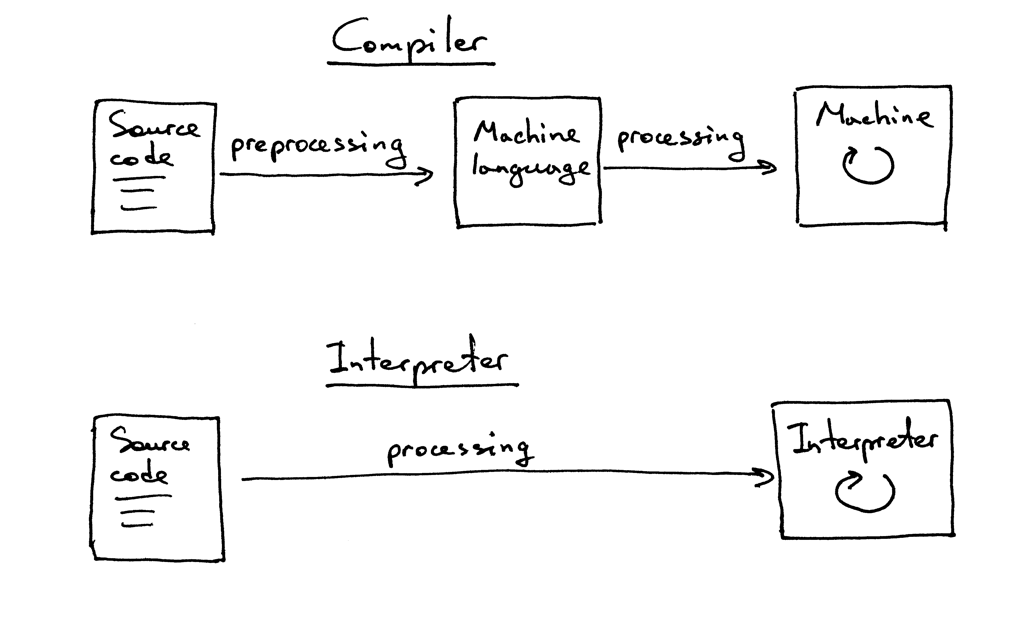
我们认为如果一个翻译器把源程序翻译成了机器语言, 那么它就是一个编译器.
如果一个翻译器处理并执行源程序而不用先把它翻译成机器语言, 那么它就是一个解释器.
看上去就像这样:
我希望到目前为止你已经确定自己真的想学习并构建一个解释器和编译器. 你期望从这个关于解释器的系列中获得什么呢?
这么说定了. 你和我将会给 Pascal 语言的一个大的子集创建一个简单的编译器. 在这个系列的最后你会有一个可以工作的 Pascal 解释器和一个就像 Python pdb 的源码级别的调试器.
你可能会问, 为什么是 Pascal? 首先, 它不是我仅仅为这个系列捏造出来的语言: 它是一个有很多重要的语言结构的真实编程语言. 并且一些老旧但是有用的计算机书籍在例子中使用 Pascal 语言 (我知道选择某个语言来搭建解释器的原因并不会特别引人注目, 但我认为学习非主流语言会是很好的改变 :)
这里有一个用 Pascal 写的阶乘函数, 你将会使用自己的编译器编译, 并使用自己创造的交互式源码级别的调试器来调试.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
program factorial;
function factorial(n: integer): longint;
begin
if n = 0 then
factorial := 1
else
factorial := n * factorial(n - 1);
end;
var
n: integer;
begin
for n := 0 to 16 do
writeln(n, '! = ', factorial(n));
end.
实现这个 Pascal 解释器的语言会是 Python, 但你可以使用你想用的任何语言, 因为这里展现的想法并不取决于任何特定的实现语言. 好吧, 让我们开始着手吧. 准备, 出发!
通过编写一个简单的算术表达式解释器, 即计算器, 你会开始对解释器和编译器的第一次尝试. 现在目标非常简单: 让你的计算器能处理两个一位整数的加法, 如 3+5. 这是一个你的计算器的源码, 抱歉, 是解释器:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, EOF = 'INTEGER', 'PLUS', 'EOF'
class Token(object):
def __init__(self, type, value):
# token type: INTEGER, PLUS, or EOF
self.type = type
# token value: 0, 1, 2. 3, 4, 5, 6, 7, 8, 9, '+', or None
self.value = value
def __str__(self):
"""String representation of the class instance.
Examples:
Token(INTEGER, 3)
Token(PLUS '+')
"""
return 'Token({type}, {value})'.format(
type=self.type,
value=repr(self.value)
)
def __repr__(self):
return self.__str__()
class Interpreter(object):
def __init__(self, text):
# client string input, e.g. "3+5"
self.text = text
# self.pos is an index into self.text
self.pos = 0
# current token instance
self.current_token = None
def error(self):
raise Exception('Error parsing input')
def get_next_token(self):
"""Lexical analyzer (also known as scanner or tokenizer)
This method is responsible for breaking a sentence
apart into tokens. One token at a time.
"""
text = self.text
# is self.pos index past the end of the self.text ?
# if so, then return EOF token because there is no more
# input left to convert into tokens
if self.pos > len(text) - 1:
return Token(EOF, None)
# get a character at the position self.pos and decide
# what token to create based on the single character
current_char = text[self.pos]
# if the character is a digit then convert it to
# integer, create an INTEGER token, increment self.pos
# index to point to the next character after the digit,
# and return the INTEGER token
if current_char.isdigit():
token = Token(INTEGER, int(current_char))
self.pos += 1
return token
if current_char == '+':
token = Token(PLUS, current_char)
self.pos += 1
return token
self.error()
def eat(self, token_type):
# compare the current token type with the passed token
# type and if they match then "eat" the current token
# and assign the next token to the self.current_token,
# otherwise raise an exception.
if self.current_token.type == token_type:
self.current_token = self.get_next_token()
else:
self.error()
def expr(self):
"""expr -> INTEGER PLUS INTEGER"""
# set current token to the first token taken from the input
self.current_token = self.get_next_token()
# we expect the current token to be a single-digit integer
left = self.current_token
self.eat(INTEGER)
# we expect the current token to be a '+' token
op = self.current_token
self.eat(PLUS)
# we expect the current token to be a single-digit integer
right = self.current_token
self.eat(INTEGER)
# after the above call the self.current_token is set to
# EOF token
# at this point INTEGER PLUS INTEGER sequence of tokens
# has been successfully found and the method can just
# return the result of adding two integers, thus
# effectively interpreting client input
result = left.value + right.value
return result
def main():
while True:
try:
# To run under Python3 replace 'raw_input' call
# with 'input'
text = raw_input('calc> ')
except EOFError:
break
if not text:
continue
interpreter = Interpreter(text)
result = interpreter.expr()
print(result)
if __name__ == '__main__':
main()
把上面的代码保存为 calc1.py 文件或者直接从 GitHub 下载. 在你开始深入代码之前, 在命令行中执行计算器, 看看它的行为. 玩玩儿它!
这是我笔记本上的一个简单例子
(如果你想用 Python3 运行这个计算器, 需要使用 input 替换 raw_input ):
1
2
3
4
5
6
7
8
$ python calc1.py
calc> 3+4
7
calc> 3+5
8
calc> 3+9
12
calc>
为了使这个简单的计算器正常工作而不抛出异常, 你的输入需要遵守如下规则:
- 输入必须是单个整数
- 暂时只支持加法运算
- 不允许输入任何空格字符
这些限制使得这个计算器很简单. 不用担心, 你很快就会使它变得复杂.
好了, 现在让我们深入并且看看你的解释器怎样工作以及它怎样计算算术表达式.
当你在命令行中输入一个表达式 3+5, 你的解释器的到了一个字符串 “3+5”. 为了解释器能真正理解要对这个字符串做什么, 它首先需要把输入 “3+5” 分解为叫做 tokens 的组件. 一个 token 是有一个类型和一个值的对象. 例如, 对于字符串 “3”, token 的类型是 INTEGER 并且响应的值是整数 3.
把输入的字符串分解成 tokens 的过程叫做词法分析. 所以, 你的解释器要做的第一步是读取输入的字符并把它转换成 tokens 的输入流. 解释器做这些的部分叫做一个词法分析器(lexical analyzer), 或者简单的叫 lexer. 你可能也见过这个组件的其他名字, 比如 scanner 或者 tokenizer. 它们的意思都一样: 解释器或编译器把输入的字符转换成 tokens 流的部分.
Interpreter 类中的 get_next_token 方法就是你的词法分析器.
每次调用它, 你就会得到传递给这个解释器的输入字符创建的下一个 token.
进一步看下这个方法本身, 看看它到底是如何把字符转换成 tokens 的.
输入保存在变量 text 中, text 保存了输入的字符串, pos 是这个字符串的一个索引
(把这个字符串当作一组字符). pos 初始化为 0 并指向字符 '3'.
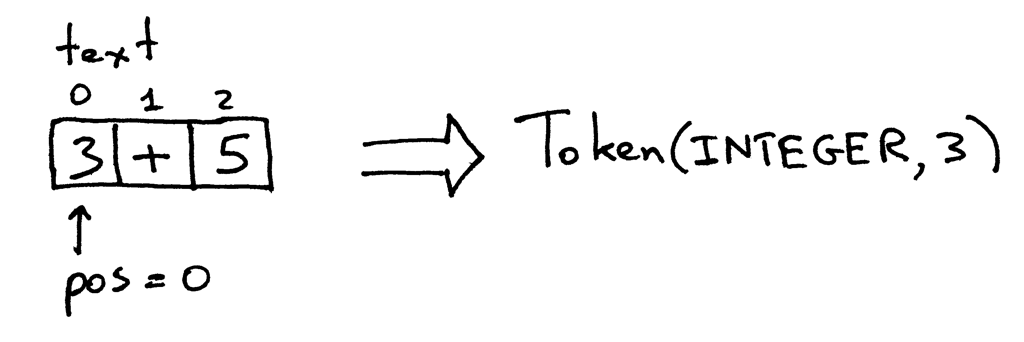
这个方法首先检查这个字符是不是一个整数, 如果是,
那么增加 pos 并返回一个类型是 INTEGER 值为字符串'3'的整数值也就是 3 的 token 实例:
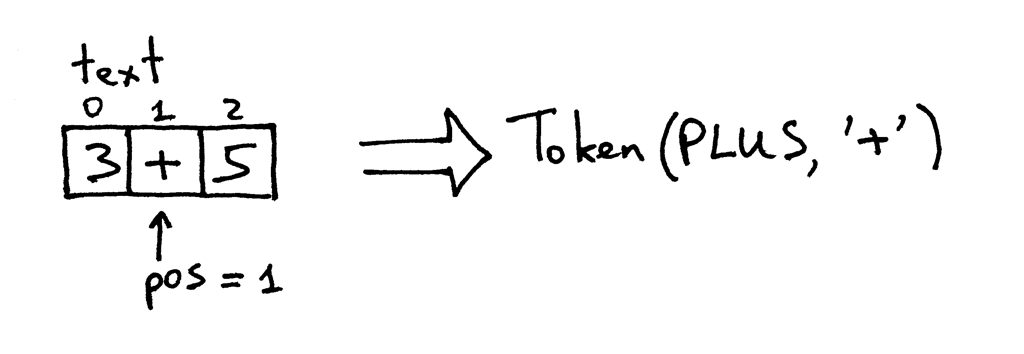
pos 现在指向 text 中的 '+' 字符. 下次你调用这个方法的时候, 它检查 pos 这个位置的字符是不是一个整数,
然后检查它是不是加号, 嗯它就是加号. 因此 pos 再加一并返回一个新创建的 token, 类型为 PLUS 值为 '+':
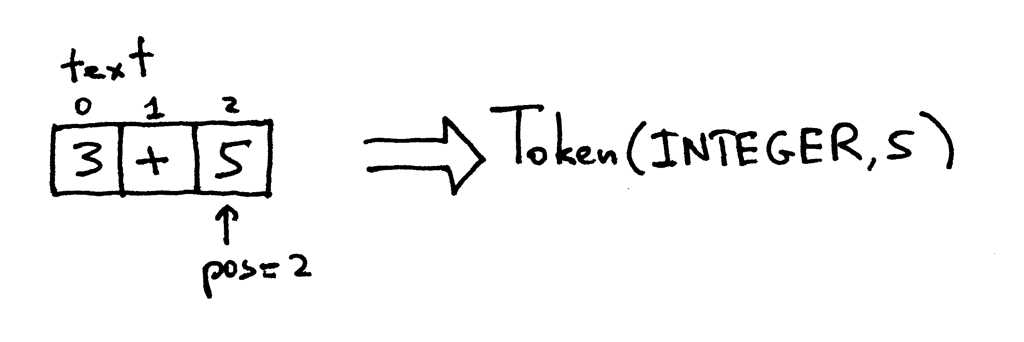
pos 现在指向了字符 '5'. 当你再调用 get_next_token 方法时, 这个方法检查它是否是一个整数,
嗯它就是, 所以增加 pos 并返回一个新的 INTEGER token, token 的值为整数 5:
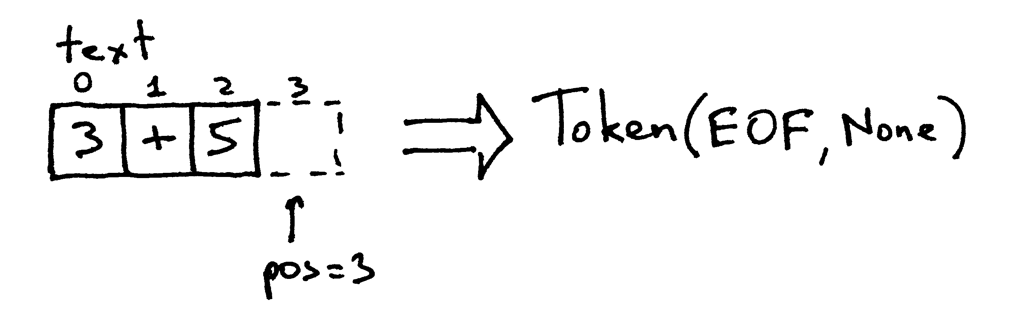
因为 pos 索引现在传递了字符串 “3+5” 的末尾, get_next_token 方法每次调用的时候就返回 EOF token:
试一试看看你的计算器的词法分析部分是如何工作的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> from calc1 import Interpreter
>>>
>>> interpreter = Interpreter('3+5')
>>> interpreter.get_next_token()
Token(INTEGER, 3)
>>>
>>> interpreter.get_next_token()
Token(PLUS, '+')
>>>
>>> interpreter.get_next_token()
Token(INTEGER, 5)
>>>
>>> interpreter.get_next_token()
Token(EOF, None)
>>>
现在你的解释器可以接触到输入字符组成的 tokens 流, 然后解释器需要处理它一下:
它需要找到从词法分析器 get_next_token 获取的流的结构. 解释器希望再流里找到如下结构:
INTEGER -> PLUS -> INTEGER. 也就是, 它试图去找到一列 tokens: 整数后面跟着加号后面跟着一个整数.
负责找到并解析这个结构的方法是 expr. 这个方法验证 tokens 序列确实和期望的 tokens 序列对应, 如 INTEGER -> PLUS -> INTEGER.
之后它成功地确认了这个结构, 通过把 PLUS 左边和右边的值加起来得到结果, 因此成功地解析了你传给这个解释器的算术表达式.
expr 方法本身使用 eat 方法来验证传递给 eat 方法的 token 类型匹配当前的 token 类型.
匹配传递的 token 类型之后 eat 方法获取下一个 token 并把它指派给 current_token 变量,
因此有效地”吃掉”现在匹配的 token 并前置 tokens 流中假想的指针.
如果流中的结构和 INTEGER PLUS INTEGER 的 tokens 序列结构不对应, 那么 eat 方法抛出一个异常.
让我们再概况一下你的解释器做了什么来计算一个算术表达式:
-
解释器接受一个输入的字符串, 假设为 “3+5”
-
解释器调用
expr方法来找到由词法分析器get_next_token返回的 tokens 流里的一个结构. 它试图找到的结构为 INTEGER PLUS INTEGER. 之后它验证这个结构, 通过相加两个 INTEGER tokens 的值来解析输入因为解释器现在知道它需要做的是相加两个整数, 3和5.
恭喜你. 你刚刚学会了构建你的第一个解释器!
现在是练习时间.

你不会认为你已经读了这篇文章然后这就够了对吧? 好吧, 着手做下面的练习吧:
-
修改代码允许输入多位整数, 例如 “12+3”
-
增加一个方法跳过空白字符这样你的计算器可以处理有空白字符的输入如 “ 12+3”
-
修改代码把 ‘+’ 改为 ‘-‘ 来计算减法如 “7-5”
检验你的理解
-
什么是一个解释器?
-
什么是一个编译器?
-
解释器和编译器有什么区别?
-
什么是一个 token ?
-
把输入分解成 tokens 的过程叫什么?
-
解释器中做词法分析的部分叫什么?
-
一个解释器或编译器那部分的常见名字有哪些?