2-3-4 Tree 与红黑树
首先我们来看 wikipedia 上对红黑树的描述, 特别是 “性质” 这一节.
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
有没有觉得看得很晕? 为什么要分成红黑两种颜色? 为什么有这些额外要求? …
而且网上大部分关于红黑树的教程都是这样描述的. ( 是的所以才会有一种红黑树很难的错觉! )
前段时间继续看了一些 算法, 第三章 Searching 部分从二叉树讲到二叉查找树讲到 2-3 树. 然后发现咦这个是不是红黑树了?
这本书可以说非常的好懂了, 由浅入深.
所以还是打算写一篇笔记, 关于如何入门红黑树.
2-3 Tree
假设大家都已经熟悉二分查找树了.
2-3 Tree 的结构如上图. 每个节点有两种类型: 2-node 或者 3-node.
2-node 指的是该节点下有两个 link, 3-node 是三个 link.
对于 2-node, 左边的 link 下的节点的值都比该节点的值小, 右边 link 下的节点的值都比该节点的值大.
对于 3-node, 该节点左边的值小于右边的值; 左边的 link 下的节点的值都比该节点左边的值小, 中间 link 下的节点的值在该节点两个值之间, 右边 link 下的节点的值都比该节点右边的值大.
Insert
插入操作, 首先按上述定义, 和二分查找树一样, 找到需要插入的值所在的节点.
如果该节点是一个 2-node, 那么直接插入该值, 节点变成 3-node.
如果该节点已经是一个 3-node, 那么插入之后就会变成 4-node. 然后转换一下, 把中间的值提出来放到它的父节点, 这样这个节点就恢复了 3-node. 父节点如果变成了 4-node 按同样操作.
如下图所示.
2-3 Tree to Red-black BST
那么上面的 2-3 Tree 怎么用二叉树的形式表示呢?
如上图所示, 对于一个 3-node 节点, 我们把它拆成两个节点并用红色的线连接. 普通节点直接的线还是黑色的.
另外 Red-black BST 有三个限制:
- 红色的线都是朝左的. 如果在插入/删除过程中朝右了需要通过旋转让红色的线保持朝左.
- 没有两个红色的线会连在同一个节点上. (也就是 4-node, 需要转成 2-3 node)
- 这棵树是完美黑色平衡( perfect black balance ) 的: 从根节点到任意一个 null link 的黑色 link 数目都是相同的
每个节点的数据结构如下, 用 color 标记该节点到父节点的 link 颜色.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node
{
Key key;
Value val;
Node left, right; // subtrees
int N; // # nodes in this subtree
boolean color; // color of link from parent to this node
Node(Key key, Value val, int N, boolean color) {
this.key = key;
this.val = val;
this.N = N;
this.color = color;
}
}
2-3-4 Tree
那么有了上面的基础, 2-3-4 Tree 也很好理解了. 即在之前 2-3 Tree 的基础上除了 2-node 和 3-node, 还有 4-node .
Top Down Insertion
对于 2-3-4 Tree, 插入一个新元素的时候, 如果一个节点已经是 4-node 了, 那么需要把这个 4-node 拆成两个 2-node.
其中把 4-node 中间的那个元素上提, 放到它之前的父节点里. 如下图所示:
自顶向下遍历该树的过程中, 如果碰到了任何 4-node 都需要把它拆成 2-node.
这样在插入过程中就不会碰到需要插入的节点是一个 4-node 而它的父节点也是一个 4-node.
Red-Black Tree
2-3-4 Tree 和 2-3 Tree 一样同样有结构复制的问题, 那么如何使用普通的二叉树表示呢?
这就是红黑树.
红黑树是一个二分查找树, 有如下特性:
- 边是红色或黑色
- 根节点到任意叶子节点的路径不会有两个连续的红边
- 根节点到任意叶子节点的路径上黑边的数量是相同的
- 连接叶子节点的边都是黑色
对于 2-3-4 Tree, 可以用如下结构表示红色树:
2-node 使用一个节点表示. 两个边都是黑色.
3-node 使用两个节点表示. 左边的节点是右边节点的父级节点或右边节点是左边节点的父节点, 两个连接的边是红色, 其他边是黑色.
4-node 使用三个节点表示. 中间的节点是左右两个节点的父节点, 连接的边是红色, 其他边是黑色.
如下图所示:
Insertion
向红黑树中插入一个新节点的时候, 先按照标准的二分查找树找到这个节点所在的叶子节点位置.
然后用新节点的值替换该叶子节点, 并把它的入边标记为红色.
给这个节点增加两个新的叶子节点, 并把叶子节点入边标记为黑色.
如果该节点的父节点的入边也是红色, 那么就会有两个连续的红边了. 需要通过旋转消除掉这两个连续的红边.
旋转方式如下:
Boom-Up Rebalancing
对于上面插入新节点的情况, 如果该节点的父节点的入边是红色并且父节点的兄弟节点的入边也是红色, 那么需要把这两条边变成黑色, 然后把父节点的父节点的入边变成红色.
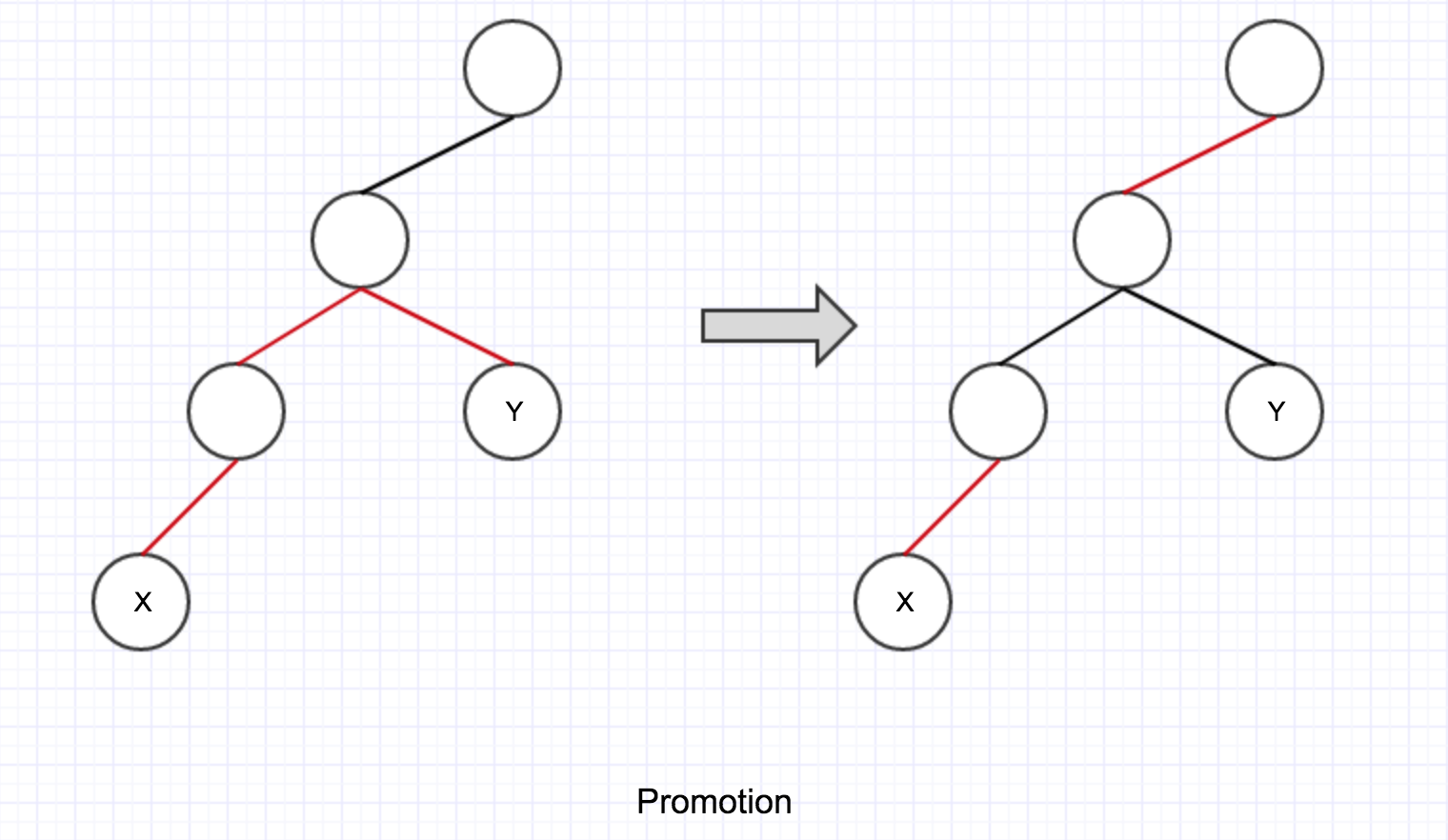
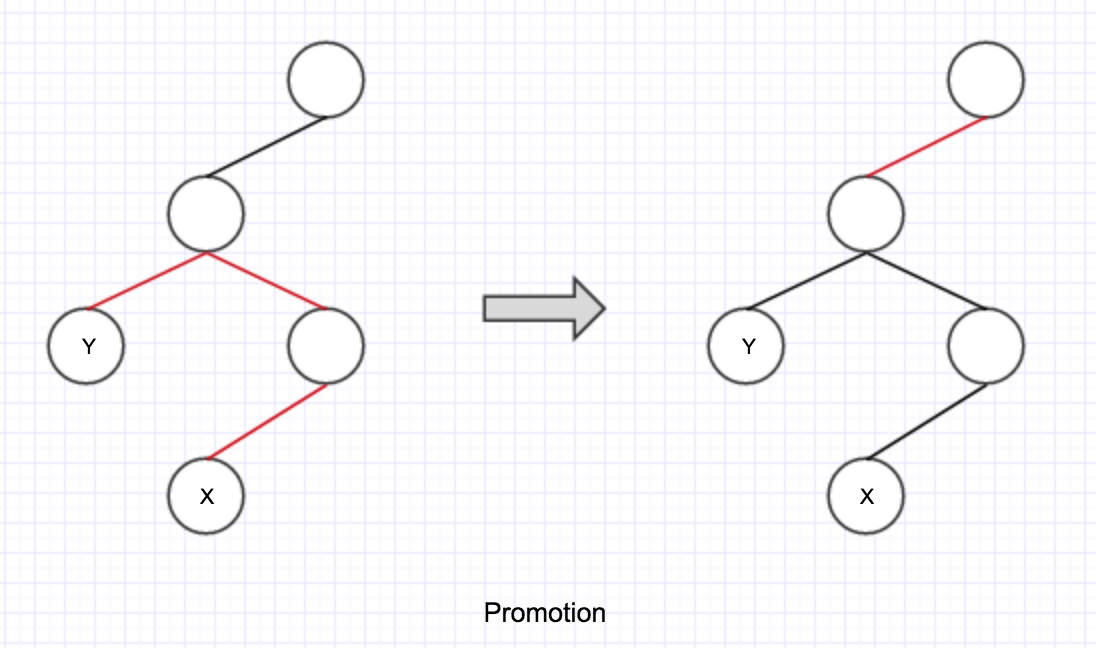
如下图所示, 蓝色节点的入边为红色而它的父节点-绿色节点的两个入边也均为红色, 于是绿色节点的父节点-灰色节点的入边提升成了红色而绿色节点的两个入边变成了黑色:
这种情况叫做 promotion.
综上, 如果有两个连续的红边, 要么旋转重构, 要么 promotion .
这一篇只是很简单的关于红黑树的基础知识介绍, 具体的实现还需要实践实践啦.
update at 2018.03.16
Java TreeMap 的具体实现
理论介绍完了之后我们来看下 Java 的一个数据结构 TreeMap 里对红黑树的具体实现.
put
TreeMap 的 put 操作里, fixAfterInsertion(e); 执行前的一部分代码是正常的 BST 找到新结点的位置, 然后执行 fixAfterInsertion(e); 对红黑树进行操作.
(代码不贴了, 大家自己看 JDK 源码)
然后具体看下 fixAfterInsertion 的操作.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/** From CLR */
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
新节点的边置为红色. while 循环内部的逻辑如下.
1.1
第一个 if 内部并且 colorOf(y) == RED 的情况, 对应上述介绍里的 promotion.
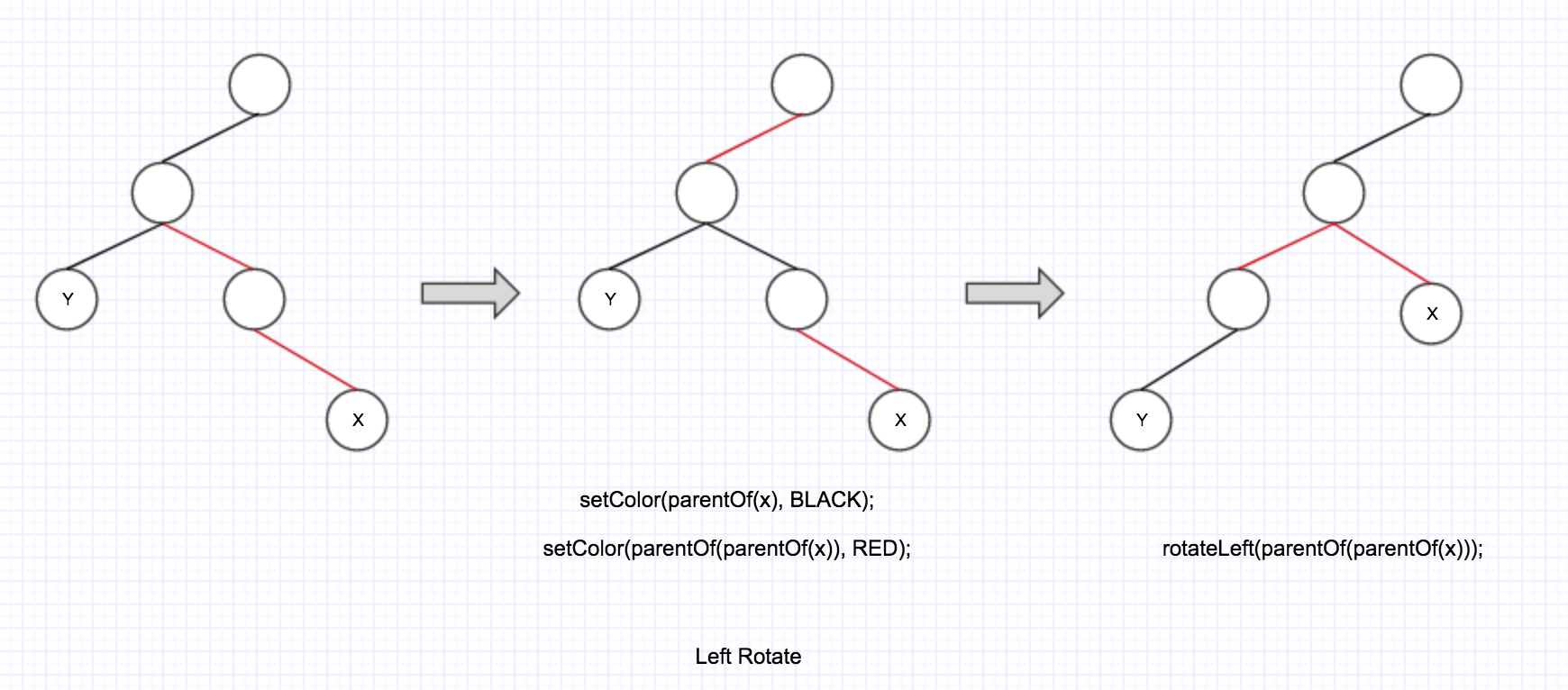
1.2
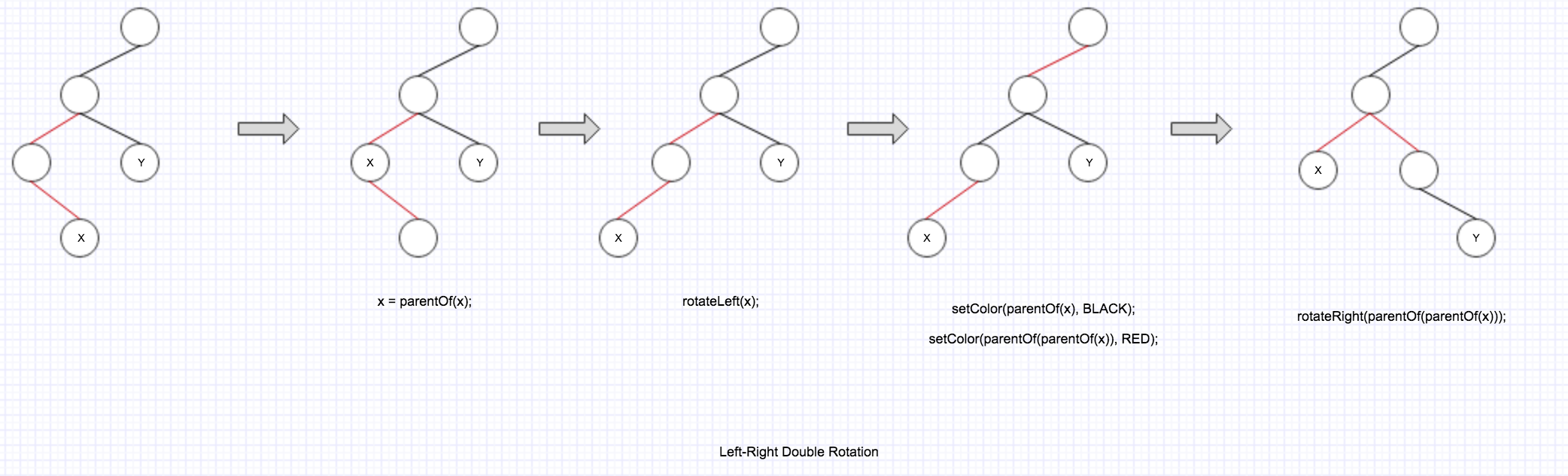
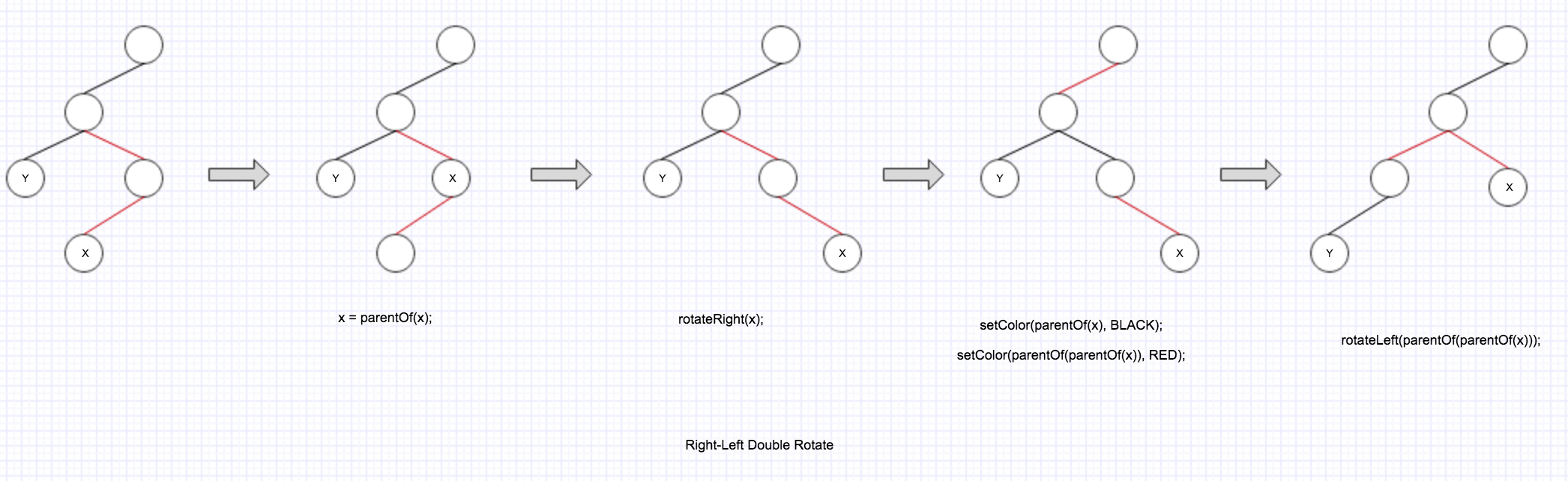
第一个 if 内部并且 colorOf(y) == BLACK 的情况, 如果 x 是它父节点的右子节点, 那么对应上述介绍里的 Left-Right Double Rotation.
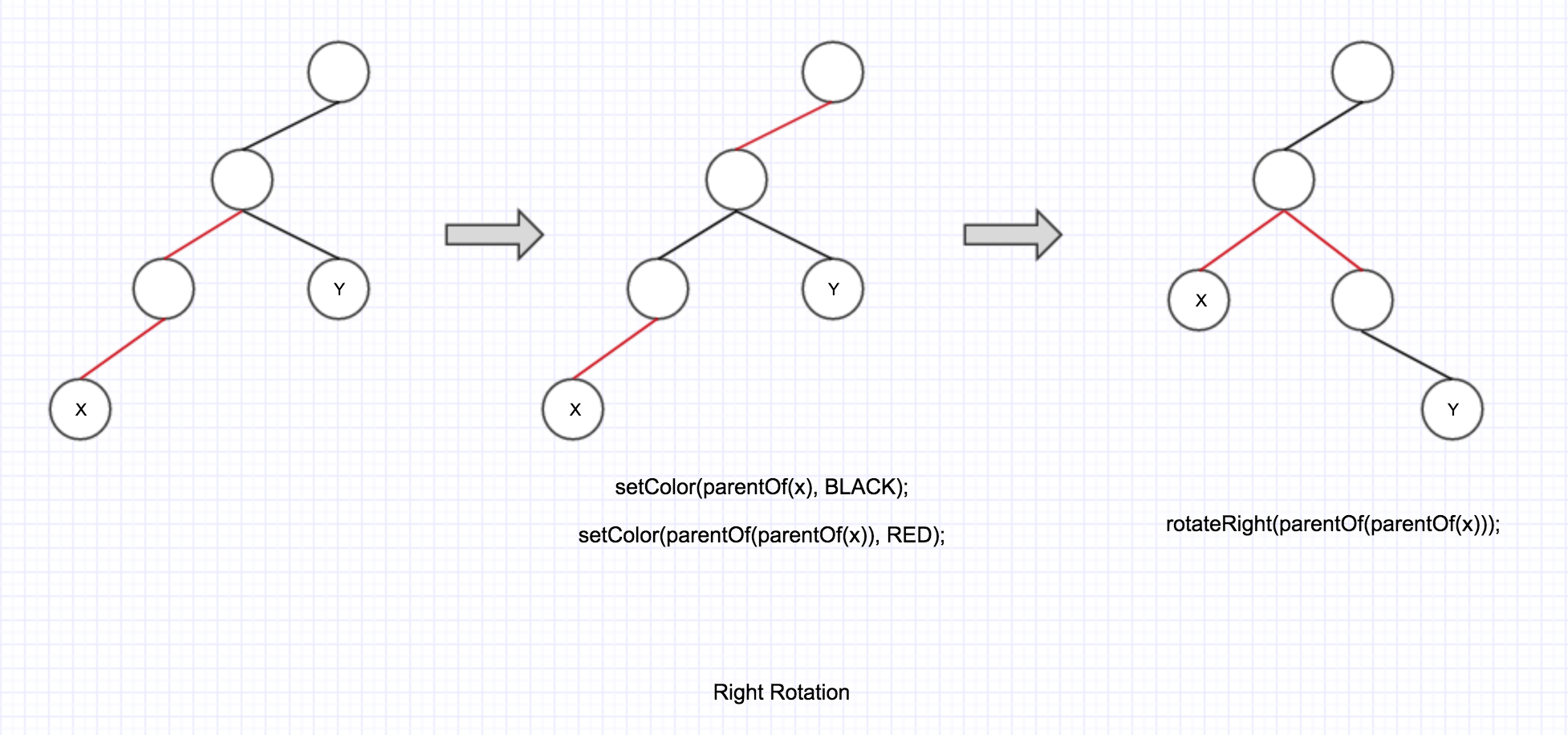
1.3
第一个 if 内部并且 colorOf(y) == BLACK 的情况, 如果 x 是它父节点的左子节点, 那么对应上述介绍里的 Right Rotation.
1.4
第一个 if 的 else 情况并且 colorOf(y) == RED, 此时和 1.1 相同, 对应 promotion.
1.5
第一个 if 的 else 情况并且 colorOf(y) == BLACK, 如果 x 是它父节点的左子节点, 那么对应上述介绍里的 Right-Left Double Rotation.
1.6
第一个 if 的 else 情况并且 colorOf(y) == BLACK, 如果 x 是它父节点的右子节点, 那么对应上述介绍里的 Left Rotation.